To achieve [O1], we will carry out an exhaustive literature review to identify the key existing MARL and control solutions to the problem of controlling the collective behaviour of complex multi-agent systems highlighting their advantages and limitations. The goal will be to identify those that are most apt to solve SAR problems, so as to collect a set of strategies to be used to benchmark those that we will develop within the project. To this aim, we will define a set of appropriate metrics to evaluate the performance of existing solutions. We envisage the definition of two sets of metrics; one to characterise the learning performance of each strategy and the second to investigate its control performance. Specifically, to evaluate the learning performance, we will define metrics to assess the overall learning time measured as the number of episodes required for the learning process to converge, the average value of the cost function during learning and its final value. To evaluate control performance we will use a set of testbed problems (see [O3]) computing for each strategy metrics assessing their stability and robustness. We will compute such metrics both locally for each agent in the group and globally as an average of all the agents in the ensemble to characterise their performance as a group.
To achieve [O2], we will look at extending the control-tutored (CT) approach to learning we recently presented in De Lellis et al., arXiv:2112.06018, 2021, where, to achieve the control of a single system of interest, a tabular learning strategy (e.g. Q-Learning) is combined with a state feedback controller to achieve better learning and control performance (see Figure 1). We named the resulting strategy as “Control-Tutored Reinforcement Learning” (CTRL). Therein, the controller is designed assuming limited knowledge of the uncertain system of interest and a policy is proposed that, according to some criterion, selects at each step either the action suggested by the tabular strategy or that suggested by the controller. In particular, we explored both the use of a deterministic criterion and of a probabilistic one to inform the choice of the best action to take. In the deterministic setting, at each step the agent is presented with two actions (one from the tabular strategy and one from the controller) and uses the one that maximises or minimises an appropriately chosen cost function related with the control goal to be achieved. In the stochastic setting, instead, at each step the policy is selected by randomly choosing one of the two actions with a given probability. In both cases, we observed in our preliminary results, recently accepted for inclusion in this year proceedings of the influential Learning for Control workshop at Stanford (see De Lellis et al., arXiv:2112.06018, 2021), a notable reduction of the learning times and a better data efficiency of the learning process.

Figure 1 (a). Architecture of Control-Tutored Reinforcement Learning. Control-tutored RL of a single system;
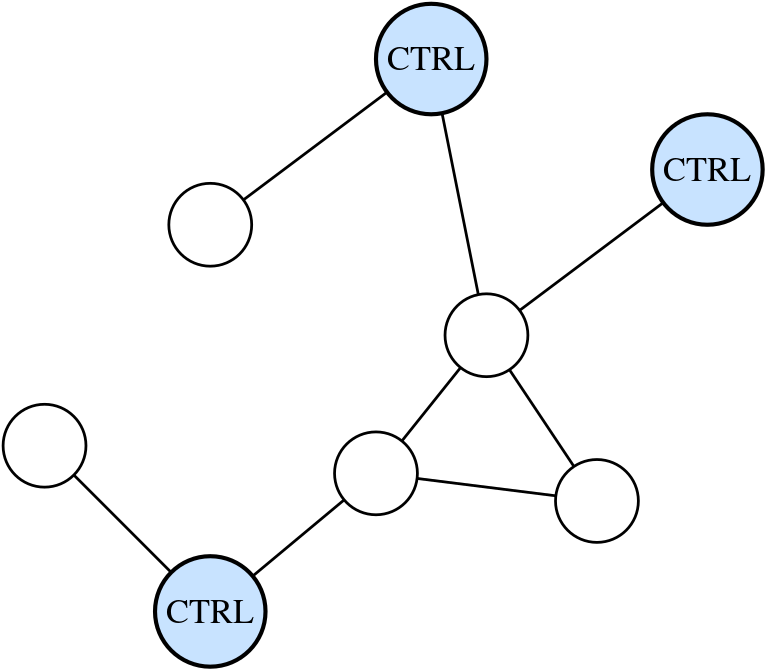
Figure 1 (b). Possible extension to multiagent scenario where some of the nodes are controlled via local CTRL strategies to steer the behaviour of the rest of the ensemble in a desired direction.
A first extension of CTRL we intend to carry out in this project is to combine Deep Reinforcement Learning (DRL) algorithms rather than tabular strategies with control tutors (developing a control-tutored DRL or CT-DRL approach) in order to achieve an even better performance, particularly in the presence of larger uncertainties and mismatches between the real system and the model used to devise the control law to be combined with the learning algorithm. The extension of these approaches to a multiagent setting seems ideal as embedding a control tutor within the strategy allows to render the learning process more effective given that the control tutor can steer the learning agent to explore a reduced search space (see De Lellis et al., arXiv:2112.06018, 2021 for some examples and performance indicators).
Therefore, our next step will be that of designing control tutored MARL strategies (CT-MARL). This will be achieved by combining existing MARL policies with distributed control strategies for network systems that have been recently presented in the literature to steer their collective behaviour. In particular, we will start with the testbed problem of achieving convergence and synchronization in complex multi-agent systems, focussing on leader-follower (or pinning control) problems as a testbed example (see for example Tang et al. Annu. Rev. Contr. 38(2):184–198 2014, Li IEEE T. Circuits I 57(1):213–224 2009, Qin et al. IEEE T. Ind. Electron. 64(6):4972–4983 2016). In this context, by exchanging information on their states/outputs with their neighbours, a fraction of the agents in the ensemble (the leaders or controllers) will need to learn how to coordinate their behaviour and what nodes to influence in the group in order to steer the collective behaviour of the ensemble on the basis of information coming only from those agents within the group they are connected to. In the spirit of CTRL, we will construct policies where each agent can select its next action either by using the action suggested by a CT-DRL algorithm running locally or that proposed by a network control system based on a (very) limited model of the agents behaviour (typically encoded in a model of the ensemble as a network of interacting nonlinear dynamical systems controlled by a relatively small fraction of controller nodes; see Yu et al. IEEE T. Automat. Contr. 57(8):2153–2158 2012 for a representative example of the model equations).
To fully leverage the benefits of CTRL strategies we will also explore the use of Hierarchical Multi Agent Reinforcement Learning (HMARL), see Ghavamzadeh et al. Auton. Agent. Multi-Ag. 13(2) 197–229 2006, to achieve more sophisticated goals such as pattern or concurrent synchronisation of different clusters of nodes on different trajectories. Specifically, we shall decompose the overall task into a set of subtasks that the agents will have to learn how to perform using control-tutored strategies. Decomposing the control objective in subtasks has several advantages, such as reducing the impact of the curse of dimensionality that affects the state-action spaces of multi-agent problems, and allowing the design of different and simpler control laws to tutor and inform the learning process of the agents in each of the subtasks.
We will explore both the use of deterministic and stochastic criteria in informing the policies that agents can use to decide their next action among those suggested by the RL or CT algorithms. We will also study the case in which different agents can use different criteria to select their policies, investigating for the first time such a heterogeneous scenario. The latter is particularly apt to orchestrate the behaviour of agents of different types (such as, for example, those being used for certain SAR operations involving the concurrent use of different types of ground and aerial vehicles). We will also investigate different architectures and training schemes, considering centralized vs decentralized training and centralized vs decentralized execution [Gronauer, S. et al, Artif Intell Rev 55, 895–943, 2022]. Another very important area to consider is the area of credit assignment in this context [Weiß G in Steels L (ed) The biology and technology of intelligent autonomous agents Springer, Berlin, pp 415–428, 1995]. One possibility is to consider for example the design of appropriate reward shaping scheme Ng AY et al, Proceedings of the Sixteenth International Conference on Machine Learning, Morgan Kaufmann, pp 278–287, 1999, the exploitation of the dependencies between agents and analysis of their actual contribution towards the global reward Kok JR et al J Mach Learn Res 7:1789–1828, 2006. Promising solutions might be those based on value decomposition networks presented in Sunehag P et al, Proc. International Foundation for Autonomous Agents and Multiagent Systems, Richland, SC, AAMAS ’18, pp 2085–2087, 2018 or QMIX Rashid T et al. in: Dy J, Krause A (eds) Proceedings of the 35th International Conference on Machine Learning, vol 80, pp 4295–4304, 2018. The integration of embedding control tutor assisted strategies in these frameworks will lead to substantial contribution from an analytical point of view. The applicants also plan to carry out extensive numerical work to support and validate the proposed models for multi-agent settings. This will also lead to the development of testing environments, which will be released as open source software.
We will achieve [O3] by carrying out the analysis of all the strategies developed in the project, with the aim of (i) assessing their convergence and robustness properties, and (ii) establishing what properties the learning agents inherited from those encoded in the tutoring control algorithms used to inform the learning. We will start with an extensive numerical analysis of their properties by using a set of representative multi-agent testbed applications, which will be used as benchmarks. In particular, we plan to use the following two problems of increasing complexity:
A) Synchronization: given a group of agents each endowed with an oscillator described by an uncertain nonlinear vector field, the control problem will be that of achieving asymptotic convergence of all the agents towards a common asymptotic solution. As this is a typical benchmark problem in the complex multi-agent systems’ literature, we will use both Kuramoto and chaotic oscillators as benchmark problems investigating how the CT-MARL strategies developed within the project solve the problem of making agents decide to what other agents they need to connect and how strongly in order to achieve a common solution.
B) Multiagent Herding: the problem will be for a group of autonomous mobile agents to cooperate in order to collect and herd a group of target agents towards a goal region in the plane (2D) or in space (3D) and maintain them confined therein.
The two benchmark problems above will be used to test and validate the robustness and convergence properties of the proposed strategies and compare their performance with respect to those of existing strategies identified as part of [O1], which will also be implemented and tested on the same application problems. The former will allow direct comparison of our strategies with the many existing in the literature to solve synchronization problems while the latter will be instrumental, as explained below, to identify the strategy which is best suited for the SAR applications of interest.
In addition to the numerical analysis described above, we will also seek to extend theoretical convergence approaches that were successfully used to investigate other RL methods to the case of the novel MARL strategies developed within the project. In particular, we will start from Sutton and Barto Reinforcement learning: an introduction MIT Press 2018, Bertsekas - Reinforcement learning and optimal control - Athena Scientific 2019, Fan et al. Learning for Dynamics and Control (L4DC) p. 486-489, 2020. and design the strategies so that a similar set of arguments could be used to prove their convergence using a combination of tools from stochastic control and dynamic programming. We will prove convergence via the design of ad hoc reward functions, such that a criterion can be established to relate the abilities of the learning agent to the stability properties of the learnt control policies via a suitable value function (for example based on a suitable Lyapunov function De Lellis et al., arXiv:2112.06018, 2021 or, more generally, a criterion based on contraction theory as recently suggested in Tsukamoto et al, Annual Reviews of Control Vol 52 2021 p. 135-169). In so doing, it will be possible to shorten the learning process by terminating it when an acceptable, yet stable, control solution is found even if it is suboptimal.
The result of our study will be a set of CT-MARL strategies and a characterization of their performance both from a learning and a control viewpoint. To achieve [O4], we will select the strategy that performed the best to solve the herding problem and further extend it to make it suitable to perform multi-agent SAR operations in uncertain environments following natural disasters. As a representative scenario we will consider the problem of controlling a possibly large number of autonomous agents (drones, underwater or ground vehicles) tasked with the goal of isolating and corralling a group of target agents (people or animals in danger) displaced over a region of interest affected by a natural disaster in order to corral and guide them towards a safe zone. In this context, the autonomous agents will have to learn to cooperate in order to: (i) search the area of interest to locate target agents and (ii) collectively corral the located agents towards the safe zone. The former task will entail agents learning how to cooperatively split the area of interest in sub-regions that each will have to monitor; this can be done statically, with each being assigned a fixed area, or dynamically, with the agents redefining over time the area each is scouting for target agents. The latter task will involve each autonomous agent to learn how to corral and drive the target agents it has located towards the safe zone.
Our preliminary results on the herding problem De Lellis et al. Int. Worksh. on Cellular Nanoscale Networks and their Applications (CNNA) 2021, Auletta et al. Auton. Robot. 1–13 2022 and those by our collaborator Prof. Michael Richardson at Macquarie University in Sydney show that these are complex multi-agent decision making tasks that can be solved efficiently by humans (Prants et al. Annual Meeting of the Cognitive Science Society 43(43) 2021, Simpson et al. Conf. on Computer Supported Cooperative Work and Social Computing (CSCW) 2021, Nalepka et al. Psychol. Sci. 28.5:630–650, 2017), but can be cumbersome for autonomous agents to learn. To overcome this problem, we will use the mathematical herding models we derived in Auletta et al. Auton. Robot. 1–13 2022, Auletta et al. IFAC-PapersOnLine 54.17 105–110 2021 in order to design control tutors to be used within the CT-MARL framework designed to achieve [O2]. The idea will be to inform the agents’ learning process by reducing the otherwise impossibly huge search space via the actions suggested at each step by the multi-agent control tutor embedded in the CT-MARL strategy.
We will validate and refine the strategy by modelling the target agents as stochastic agents diffusing away from the safe zone that can be either repelled or attracted by the presence of the autonomous agents, which will have to adjust their behaviour in order to corral and push them towards the safe zone. We will investigate both the case where target agents are flocking, as it happens with some animal groups, and the case where they are not, as for example when people are involved. Removing the simplifying assumption that target agents tend to flock, which is often assumed in the existing literature Sumpter et al. IAPR Worksh. on Machine Vision Applications 1998, Haque et al. IFAC Proceedings Volumes 42.17:262–267 2009, Strömbom et al. J. Roy. Soc. Interface 11.100 20140719 2014, Paranjape et al. IEEE T. Robot. 34.4:901–915 2018, Chipade, IEEE T. Robot. 37.6:1956–1972 2021, will represent an important advance with respect to the current state of the art that would be difficult to achieve without machine learning. Another challenge is to ensure that the agents cooperatively learn the right model for navigation in unstructured environments without complete knowledge of the latter and of the states of all the agents.
Exploiting the CT-MARL strategies developed within the project can automatically embed the agents with exploration capabilities to deal with unknown environments and to deal with the situation when the assumption of flocking is removed. The use of control-tutored strategies will render the learning times compatible with those suitable for real-world situations where agents will have to learn how to cooperate to solve the problem within a limited amount of time.
Given the time scale of the project, we plan to validate the results of the project through a combination of simulations and scale experiments. In particular, will study a variety of realistic emergency scenarios using simulations. We will develop environments for simulations and also visualization using tools like Unity. These simulations will be data-driven involving experts from civil protection and emergency services with whom we have ongoing collaborations within the scope of the Modelling and Engineering Risk and Complexity program of the Scuola Superiore Meridionale in Naples. In particular, we will consider scenarios where there are constraints given by the nature of the disaster (e.g., volcanic eruptions, earthquakes, and flooding), the morphology of the territory and the availability of rescuing agents. We believe that the results of the experiments will provide a powerful proof-of-concepts for these technologies and demonstrate their general applicability for future potential adoption and deployments, not only for SAR.
Also, as a proof-of-principle case study, we plan to deploy our strategy to solve the problem of using a group of autonomous biomimetic robots to search and rescue fish away from an environmental disaster area towards a safe zone. This work will be informed by our previous work on modelling fish behavior in terms of coupled stochastic differential equations parameterized from experimental data (see Zienkiewicz et al. J. Math. Biol. 71(5):1081–1105 2015, Zienkiewicz et al. J. Theor. Biol. 443:39–51 2018) and will be carried out in cooperation with Prof. Maurizio Porfiri and his team at the Dynamical Systems Laboratory of New York University, where scale tests and experiments with their robotic fish will also be conducted; see De Lellis et al. IEEE T. Robot. 36(1):28–41 2020 for some of our preliminary experimental results.




